Every liquid has its own vapor pressure at a given temperature. It depends upon the intermolecular forces. Whenever, a solute is dissolved in a liquid solvent then the vapor pressure of the solvent decreases. Raoult’s law has explained the relationship of vapor pressures of pure solvent, vapor pressure of solution and the amount of the solute. The amount of the solute is expressed in mole fractions.
We will discuss Raoult’s law by considering:
- When the solute is non-volatile and non-electrolyte and solvent is volatile.
- When the solute and solvent both are volatile.
Raoult’s law when solute is non-volatile and non-electrolyte (solid solute)
Raoult’s law is defined in three ways:
First Definition:
The vapor pressure of the solution is directly proportional to the mole fraction of the solvent.
\[
p \propto x_{1}
\]
\[
p = p^{\circ} x_{1} \qquad \cdots (1)
\]
- Where, P = vapor pressure of solution
- P° = vapor pressure of pure solvent
- x1 = Mole Fraction of solvent
- in order to deduce the second definition of Raoult’s law, we proceed as follows.
since, X1 + X2 = 1 (X2 is mole fraction of solute)
So, X1 = 1 – X2
Putting this value of X1 in equation (1)
p = p° (1 – x2)
p = p° – p°x2
p – p° = p°x2
As p – p° = Δp (Δp is the lowering of vapor pressure)
So Δp = p°x2 ……….(2)
Δp α x2
Second definition:
The lowering ofvapour pressure of solvant is directly proportional to the mole fraction of solute.Equation (2) can be re-arranged.
Third Definition:
The relative lowering of vapor pressure is equal to the mole fraction of solute.
The relative lowering of vapor pressure has three important characteristics.
- It is independent of the temperature.
- It is proportional to the concentration of solute.
- It is a constant quantity when equi-molecular proportions of different solutes are dissolved in same mass of the same solvent.
Graphical explanation of Raoult’s law
In order to give the graphical shape to equation (4), let us prepare nine different solutions with the following compositions:

All these nine solutions have their own vapor pressures. These values of vapor pressures are the sum of vapor pressures of components in solution state.
Let us plot a graph between mole fractions of A and B on x-axis and vapor pressures of solutions on y-axis. When all the solutions behave ideally, then a straight line is obtained. Actually equation (4) is the equation of a straight line.
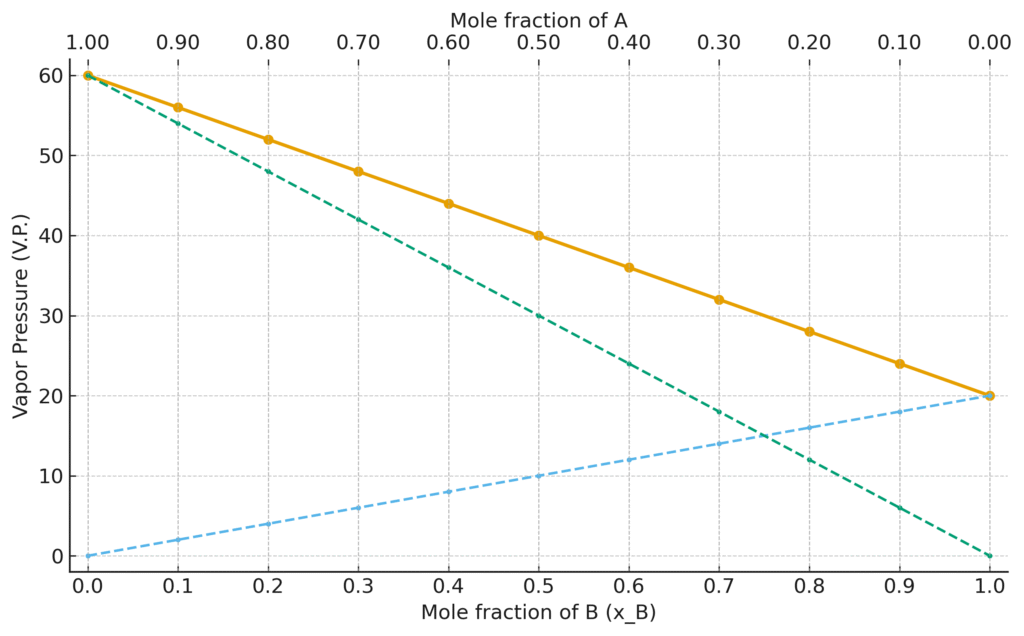
The value of mole fractions of A decrease from left to right. The values of mole fractions of component B, increase from left to right. PB° is the vapor pressure of the pure component B. A is a low boiling liquid, pa° is the vapor pressure of the pure component A. B is a high boiling liquid. That is why its vapor pressure is less.
The values of the vapor pressures of all the nine solutions are on the straight line joining the two pure components. So, all such solutions are ideal solutions, according to Raoult’s Law.
Raoult’s law when both components are volatile
Suppose we have two liquids A and B. Let their vapor pressures be PA° and PB° in the pure state at a given temperature. After making the solutions the vapor pressure of both the components are changed. Let the vapor pressures in the solution state are PA and PB. These values of vapor pressures are less than in pure states. Suppose their mole fractions are xA and xB.
According to the first definition of Raoult’s law
PA = PA° . XA
PB = PB° . XB
The total vapor pressure of the solution is the sum of these two vapor pressures.
Pt = pA +pB = pA° xA +pB° xB
Since xA + xB = 1
So, xB = ( 1 – xA)
Putting value of xB
\begin{align*}
P_t &= p_B^\circ (1 – x_A) + p_A^\circ x_A \\
P_t &= p_B^\circ – p_B^\circ x_A + p_A^\circ x_A \\
P_t &= p_B^\circ + (p_A^\circ – p_B^\circ) x_A \\
P_t &= (p_A^\circ – p_B^\circ)x_A + p_B^\circ \quad \cdots (4)
\end{align*}
According to equation (4), the total vapor pressure of mixture of two components A and B depends upon their pure vapor pressures and the mole fraction of the component A. The vapor pressures of pure components p°A and p°B are constant at a given temperature. The variable parameter is xA. So the total vapor pressure Pt changes with the change of xA. When, we say that the mole fraction of A changes, the mole fraction of B also changes. When the mole fraction of A increase then the mole fraction of B decreases.
